LLM可解释性的未来希望？稀疏自编码器是如何工作的，这里有一份直观说明

AIGC动态4个月前发布 almosthuman2014

803 0 0

文章摘要

稀疏自编码器（SAE）是一种在机器学习领域中越来越受重视的工具，它有助于解释和理解深度学习模型的工作原理。SAE的设计灵感来源于神经科学中的稀疏编码假设，通过将输入数据转换成稀疏的中间表示，SAE能够揭示模型内部的工作原理。

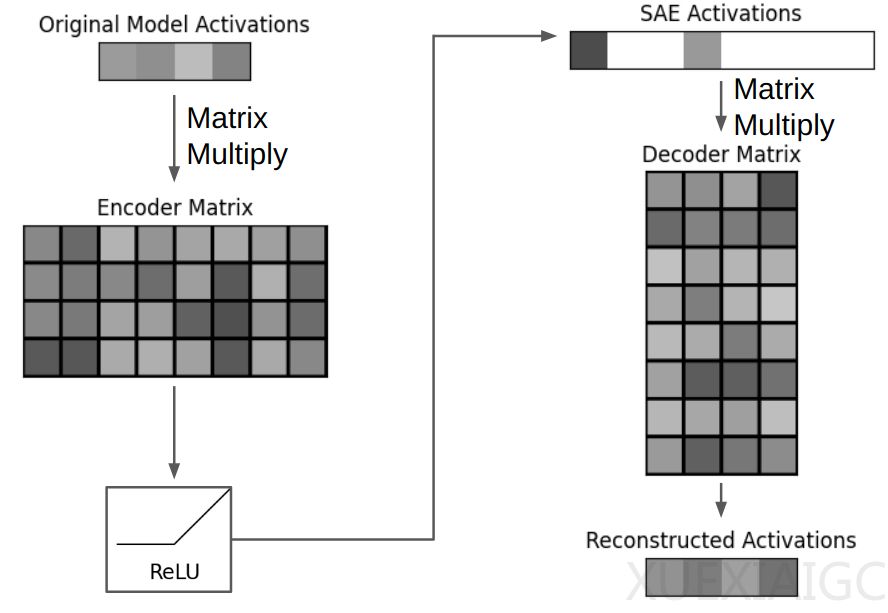
SAE的工作原理与标准自编码器类似，但增加了稀疏性约束。标准自编码器通过编码器将输入数据压缩，然后通过解码器重建输入数据。而SAE在这一过程中增加了稀疏度惩罚，促使模型创建稀疏的中间表示，即在编码后的向量中只有少数非零元素。这种稀疏性有助于我们更好地理解模型的内部表示。

SAE在大型语言模型（LLM）中的应用尤为显著。LLM通常包含数十层的神经网络，每层都会产生大量的中间激活。通过在LLM的中间激活上应用SAE，我们可以将这些高维的激活转换为更易于理解的稀疏表示。例如，GPT-3模型的某一层激活可以通过SAE被扩展到更高的维度，并通过稀疏性约束得到一个稀疏的编码表示。

SAE的一个重要应用是特征解释。理想情况下，SAE的稀疏表示中的每个非零元素都对应于一个可理解的特征。通过分析能够激活特定特征的输入，我们可以对这些特征进行解释。例如，某些特征可能与特定的概念（如“金毛犬”）相关联，而其他特征可能与更抽象的概念（如关系从句）相关。

此外，SAE还可以用于因果干预。通过调整SAE解码器向量，我们可以改变模型的输出，例如强制模型在每个响应中提及特定的概念。这种方法为理解模型行为提供了一种直观的途径。

然而，SAE的评估仍然是一个挑战。由于缺乏可度量的底层真实表示，评估SAE的可解释性通常依赖于主观判断。尽管如此，一些代理指标（如L0和Loss Recovered）被用来衡量SAE的性能。L0表示编码表示中非零元素的平均数量，而Loss Recovered衡量使用重建激活替换原始激活后的额外损失。这些指标有助于我们在稀疏性和重建准确度之间找到平衡。

尽管SAE在可解释性领域取得了进展，但仍存在许多挑战。例如，训练损失函数与代理指标之间并不直接对应，而且代理指标只是对特征可解释性的主观评估的代理。此外，LLM中的一些重要概念可能难以解释，盲目优化可解释性可能会忽略这些概念。

总之，SAE为理解深度学习模型提供了一种有前景的方法。通过揭示模型的内部表示和特征，SAE有助于我们更好地理解模型的行为，并为改进模型提供了新的途径。虽然SAE的评估和优化仍然面临挑战，但随着研究的深入，SAE有望在可解释性领域发挥更大的作用。