Transformer要变Kansformer？用了几十年的MLP迎来挑战者KAN

AIGC动态3个月前发布 almosthuman2014

364 0 0

Transformer要变Kansformer？用了几十年的MLP迎来挑战者KAN

文章摘要

【关键词】 神经网络、Kolmogorov-Arnold Networks、机器学习、深度学习、Transformer模型

本文提出了一种新型的神经网络架构——Kolmogorov-Arnold Networks（KAN），作为多层感知器（MLP）的替代方案。MLP作为深度学习模型的基础构件，尽管被广泛使用，但存在一些明显的缺陷，如在Transformer模型中参数消耗大且可解释性较差。KAN的设计灵感来源于Kolmogorov-Arnold表示定理，该定理表明多变量连续函数可以表示为单变量连续函数和二元加法运算的有限组合。

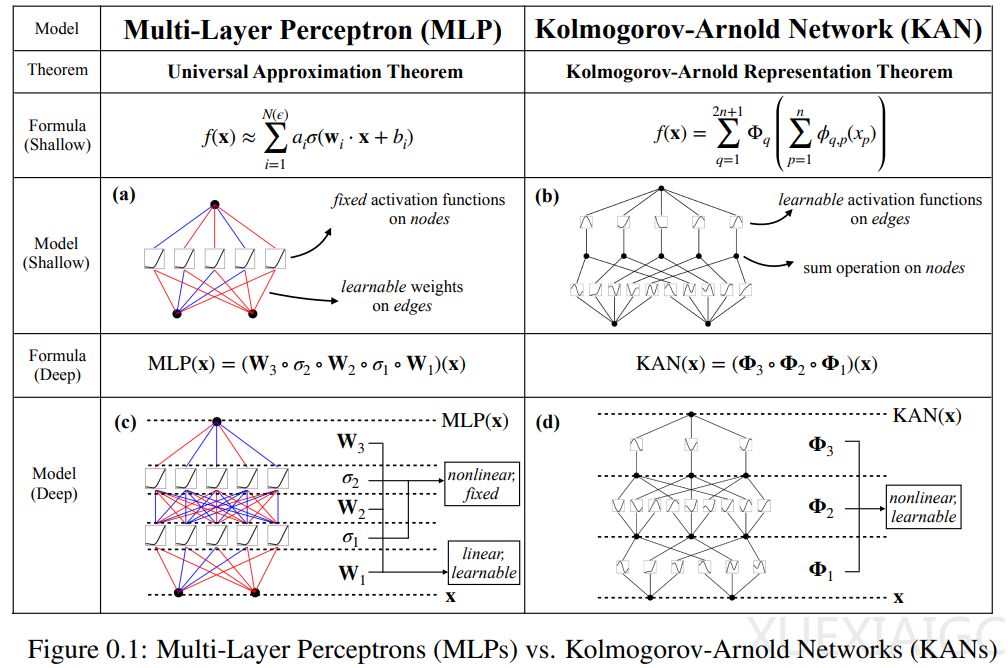
KAN与MLP都拥有全连接的结构，但KAN在边（权重）上放置可学习的激活函数，而MLP在节点（神经元）上放置固定激活函数。KAN没有线性权重矩阵，每个权重参数都被替换为一个可学习的一维函数，参数化为样条（spline）。KAN的节点仅对传入信号进行求和，而不应用任何非线性变换。这种设计使得KAN在计算图上比MLP小得多，同时在参数效率上也有所提高。

研究者通过大量实证实验展示了KAN在准确性和可解释性方面对MLP的显著改进。尽管KAN数学解释能力不错，但实际上它们只是样条和MLP的组合，利用了二者的优点，避免了缺点的出现。样条在低维函数上准确度高，易于局部调整，并且能够在不同分辨率之间切换。然而，由于样条无法利用组合结构，因此它们存在严重COD问题。另一方面，MLP由于其特征学习能力，较少受到COD的影响，但在低维空间中却不如样条准确，因为它们无法优化单变量函数。

KAN模型不仅应该学习组合结构（外部自由度），还应该很好地近似单变量函数（内部自由度）。KAN就是这样的模型，因为它们在外部类似于MLP，在内部类似于样条。结果，KAN不仅可以学习特征（得益于它们与MLP的外部相似性），还可以将这些学习到的特征优化到很高的精度（得益于它们与样条的内部相似性）。

论文还讨论了Kolmogorov-Arnold表示定理在机器学习中的实用性，指出不必坚持原始的方程，可以将网络泛化为任意宽度和深度。此外，科学和日常生活中的大多数函数通常是平滑的，并且具有稀疏的组合结构，这可能有助于平滑的Kolmogorov-Arnold表示。

总的来说，KAN作为一种新型的神经网络架构，具有在准确性和可解释性方面超越传统MLP的潜力，为深度学习领域提供了新的研究方向。论文的代码可在GitHub上获取，也可以通过pip install pykan安装。