扩散模型、最优传输存在什么关系?法国数学家4页论文引网友围观
文章摘要
【关 键 词】 扩散模型、最优传输、Fokker-Planck、生成模型、数学推导
扩散模型与最优传输之间的关系一直是一个复杂且引人入胜的研究领域。在2022年,博科尼大学的Hugo Lavenant和里昂第一大学的Filippo Santambrogio合作发表的论文《THE FLOW MAP OF THE FOKKER-PLANCK EQUATION DOES NOT PROVIDE OPTIMAL TRANSPORT》中,他们探讨了流模型在最优传输框架中的应用,并提供了一个反例,表明在某些情况下,流模型并不能实现最优传输。这一发现反驳了Khrulkov和Oseledets之前的研究中提出的一个猜想,即通过积分Fokker-Planck方程的Wasserstein速度得到的ODE流可以获得一个最优传输映射。
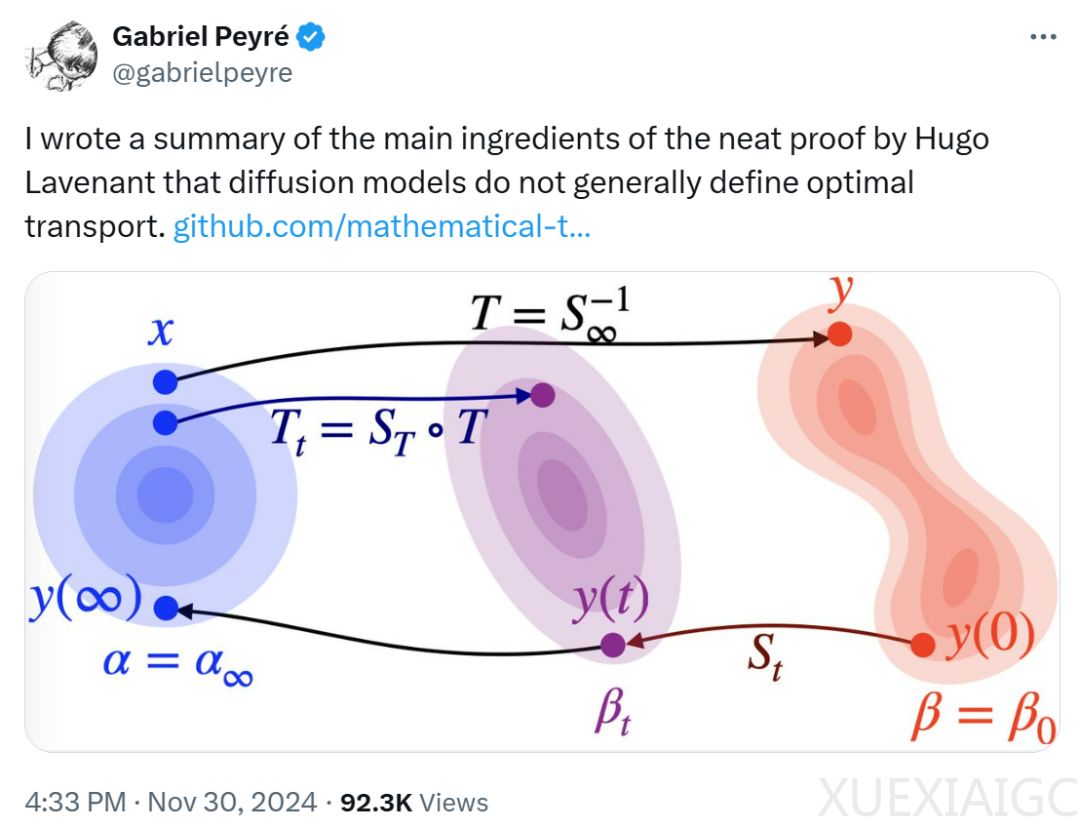
法国数学家Gabriel Peyré在其论文《Diffusion models and Optimal Transport》中对Lavenant和Santambrogio的研究进行了概括,指出扩散模型通常不能定义最优传输映射。生成模型的目标是在参考分布α(通常是各向同性高斯分布)和数据分布β之间构建传输映射T,使得T♯α = β。尽管这样的映射总是存在的,但找到T的明确构造方法却非常困难。
最优传输通过求解Monge问题来确定T,而逆向Flow Map则是扩散模型中考虑的另一种方法。Lavenant和Santambrogio通过构造一个接近各向同性高斯α的β,并证明存在某些t ≥ 0,使得从α到β_t的逆向Flow Map T_t不是最优传输,从而证明了逆向Flow Map通常不是最优传输。他们的研究结果表明,对于某些特定的t_0 > 0,T_t并不是所有t ∈ (0, t_0]的最优传输。
这一发现对于理解扩散模型和最优传输之间的关系具有重要意义,也为未来的研究提供了新的视角和挑战。通过深入分析和数学推导,Lavenant和Santambrogio的研究揭示了在某些情况下,逆向Flow Map并不能实现最优传输,这对于生成模型的设计和优化具有重要的指导意义。
原文和模型
【原文链接】 阅读原文 [ 1651字 | 7分钟 ]
【原文作者】 机器之心
【摘要模型】 moonshot-v1-32k
【摘要评分】 ★★☆☆☆




