「注意力实际上是对数的」?七年前的Transformer还有新发现,Karpathy点赞
文章摘要
【关 键 词】 注意力、复杂度、Transformer、并行计算、对数
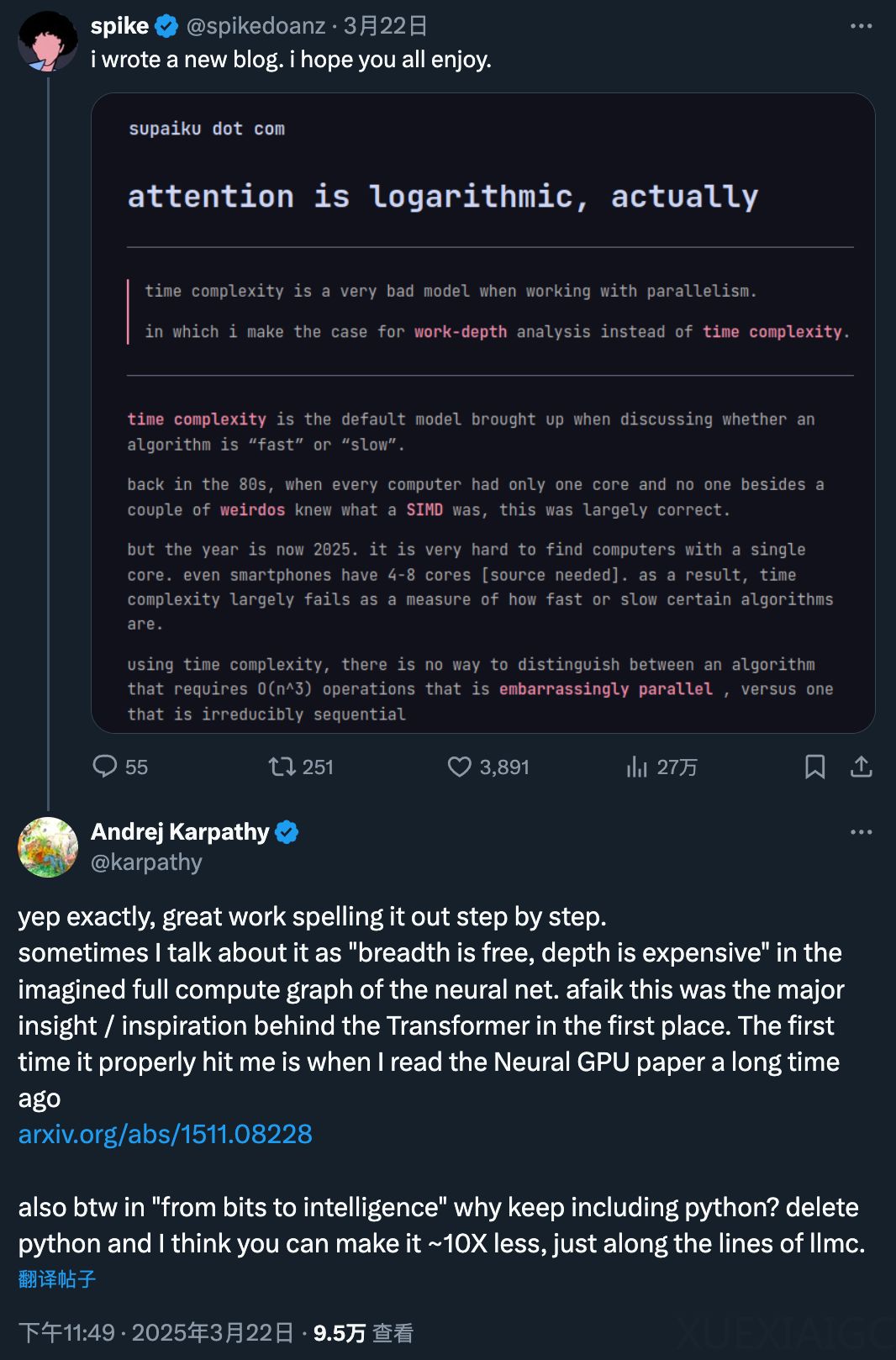
在当前的AI社区中,注意力机制的计算复杂度问题再次引发了广泛讨论。作者提出了一种全新的视角,认为Transformer中的注意力机制在计算复杂度上应被视为对数级别,而非传统的平方级别。这一观点得到了Karpathy的高度肯定,他指出“广度是免费的,深度是昂贵的”,并认为这是Transformer背后的主要灵感之一。
传统的注意力机制(如Transformer中的自注意力)的计算复杂度主要来源于点积计算和Softmax归一化,其复杂度通常被认为随着序列长度的平方增长,这也是Transformer难以处理长序列的核心瓶颈。然而,作者通过引入“work-depth模型”来分析算法的复杂度,提出了一种更全面的衡量方式。该模型不仅关注输入大小对应的操作数量,还从理论下限的角度思考算法的复杂度,特别是不可并行的顺序操作的最小数量。
通过多个案例,作者详细阐述了这一观点。例如,逐个元素相乘在单线程下是线性时间,但在并行计算下,其时间复杂度实际上是常数时间,直到达到某个临界点。类似地,向量求和操作虽然看似需要顺序执行,但通过并行化处理,其复杂度可以降低到对数级别。张量积和矩阵乘法等操作也展示了类似的特性,尤其是在并行计算环境下,其深度复杂度并不会随着数据量的增加而显著增加。
然而,作者也指出了这一模型的局限性。当内存访问模式不连续或物化变量与内存层次结构不匹配时,深度复杂度模型可能会失效。特别是在注意力机制中,QK^T矩阵的实体化可能会导致二级缓存溢出,从而使得实际的计算复杂度更接近于O(n log n)。尽管如此,作者对未来计算的发展持乐观态度,认为随着计算单元的局部性增强,神经网络的权重在训练过程中将越来越静态,这可能会进一步优化注意力机制的计算效率。
总的来说,作者通过对注意力机制的深度分析,提出了一种新的对数级别复杂度的视角,并探讨了其在并行计算环境下的应用和局限性。这一研究不仅为理解Transformer的计算复杂度提供了新的思路,也为未来的算法优化和硬件设计提供了重要的参考。
原文和模型
【原文链接】 阅读原文 [ 3450字 | 14分钟 ]
【原文作者】 机器之心
【摘要模型】 deepseek/deepseek-v3/community
【摘要评分】 ★★★★★





