为什么学线代时不知道：矩阵与图竟然存在等价关系

AIGC动态4周前发布 almosthuman2014

193 0 0

文章摘要

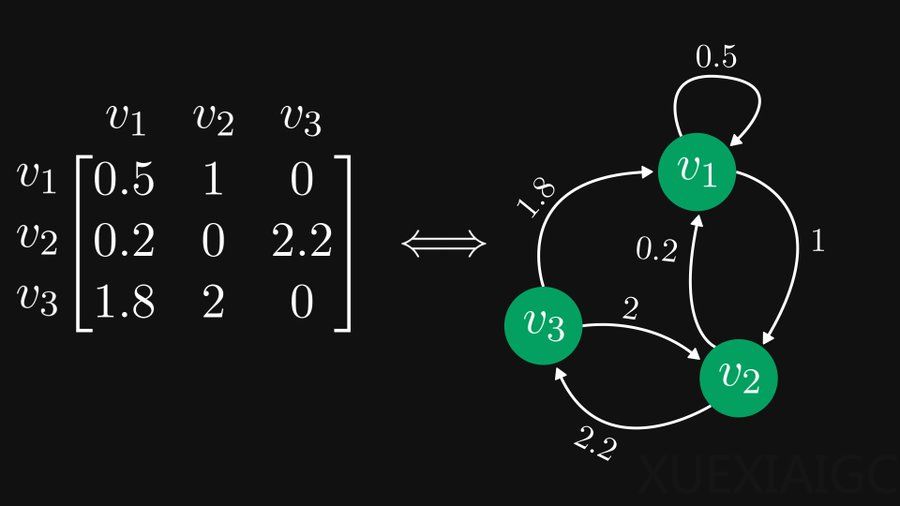
数学家 Tivadar Danka 通过其推文和博客文章，生动地介绍了非负矩阵与有向图之间的等价性及其在数学领域的应用。Danka 的介绍方式使得超过200万人通过推文了解了这一概念，获得了3200次转发和9100次收藏。在数学学习中，将矩阵的每一行视为节点，每个元素视为有向且加权的边，可以帮助我们从几何角度理解矩阵的运算，例如矩阵的幂对应于图中的游走。

Danka 强调了强连通分量在理解非负矩阵结构中的重要性。强连通分量是有向图中能够实现从每个节点到达其他每个节点的部分。对应于强连通图的矩阵是不可约矩阵，而非负矩阵中的其他矩阵都是可约矩阵。通过将包含强连通分量的图转写成矩阵形式，我们可以看到弗罗贝尼乌斯标准形（Frobenius normal form）的矩阵表示。

Danka 还介绍了如何将任意非负矩阵转换成弗罗贝尼乌斯标准形矩阵。首先构建对应的有向图，找到强连通分量，然后重新标注各个节点，最终得到弗罗贝尼乌斯标准形矩阵。这个过程可以通过使用置换矩阵对原矩阵执行变换来实现。

此外，矩阵与图之间的等价关系不仅有助于图论研究，还能为线性代数的计算和分析提供新视角。例如，矩阵的特征值可以定义图的特征值，催生了谱图理论（spectral graph theory）这一研究领域。这种等价关系在实际应用中也具有重要价值，如 DNA 数据常以矩阵或图的形式表示。

Danka 正在编写的《Mathematics of Machine Learning》一书，将由浅入深地介绍与机器学习相关的数学知识，帮助读者深入理解机器学习的原理。这本书有望成为学习机器学习的最佳资源，目前已在网上发布了两章预览，感兴趣的读者可以访问 Danka 的网站了解更多信息。通过将矩阵与图的等价关系应用于 AI 领域，可能会在 AI 可解释性和图人工智能方面带来新的突破，有助于我们更好地学习线性代数。